Theoretische Informatik

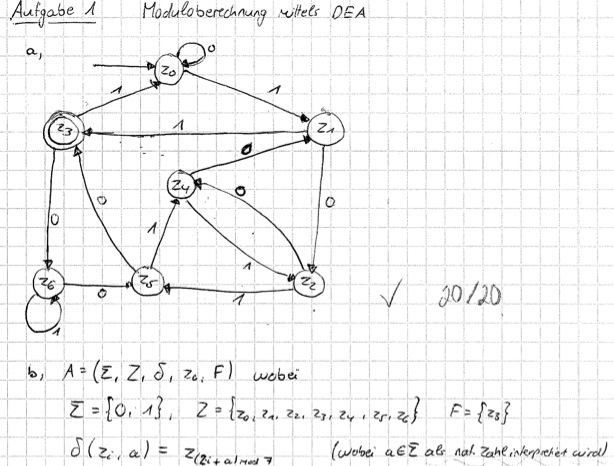
Moduloberechnung mittels DEA
Gesucht ist ein DEA mit genau 7 Zuständen, der die Menge S aller Binärzahlen, die kongruent 3 modulo 7 sind, akzeptiert (wobei führende Nullen zugelassen sind).
S={b_nbn-1···b₀􏰂􏰂n≥0,b₀,...,b_n ∈{0,1}, 􏰅b_i·2ⁱ ≡3 (mod 7)}

1. Zeichnen Sie den gesuchten DEA.
2. Geben Sie den DEA als 5-Tupel an. Definieren Sie dabei alle Komponenten vollständig und präzise (inkl. der Überführungsfunktion δ).

Schnelle Suche mit DEAs
Gesucht ist ein DEA mit 8 Zuständen und Eingabealphabet Σ = {a,b,c}, der die Sprache L = {x · v · z | x, z ∈ Σ∗, v = acbacac} akzeptiert. Gehen Sie wie im Beispiel 3.9 vor.

1. Zeichnen Sie den gesuchten DEA und geben Sie ihn in Papierform ab.
2. In den Hinweisen finden Sie den Quelltext eines Python-Programms, das DEAs simulieren kann. Die dort benutzte Codierung von DEAs als Python-Listen wollen wir auch in den folgenden Übungsblättern verwenden. Tragen Sie in der Funktion deaDefine den unter (a) erhaltenen DEA ein und geben Sie das entstandene Programm ab.

Konstruktionen für NEAs
K = Sprache u ̈ber {1, 2}, die von dem oben stehenden NEA akzeptiert wird
L = {w∈{1,2}∗ ||w|≥2 und w beginnt mit 1 und endet mit 2}
M = {w∈{1,2}∗ ||w|≥2und das vorletzte Symbol von w ist eine 1}

1. Geben Sie NEAs für L und M in grafischer Darstellung und in Tupeldarstellung an.
2. Konstruieren Sie einen DEA für K, indem Sie die Potenzmengenkonstruktion für den oben stehenden NEA durchführen. Zeichnen Sie den entstehenden DEA.
3. Konstruieren Sie, dem Verfahren aus Satz 3.20 folgend, NEAs für K, L∪M und (L∪M)·K. Zeichnen Sie die entstehenden NEAs.

Variante des Halteproblems
Beweisen Sie A ∈/ REC, wobei A = {(x,y) ∈ N×N | x ≠ y und M_x hält bei Eingabe y}.

Entscheidbarkeit der Wertebereiche von Polynomen
Sei p : Z → Z ein Polynom mit einer Variablen und Koeffizienten aus Z. Zeigen Sie W_p ∩ N ∈ REC.

komplementäre Definitions- und Wertebereiche
Beweisen Sie folgende Aussage für alle A ⊆ N:
A∈REC ⇐⇒ A ist endlich oder A=N oder
es existiert ein berechenbares φ:N→N mit D_φ = A und W_φ =(A KOMPLEMENTAER)