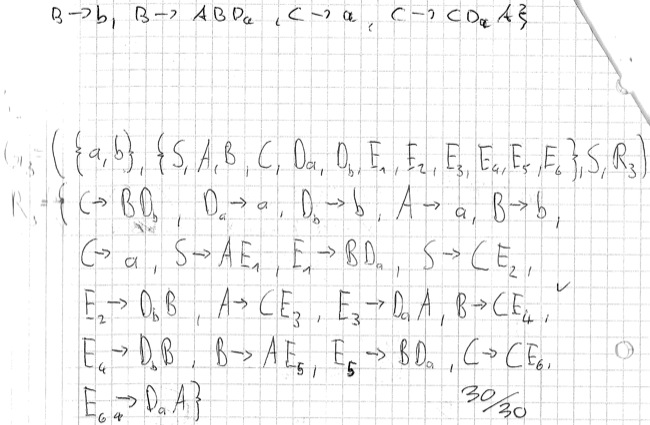Theoretische Informatik

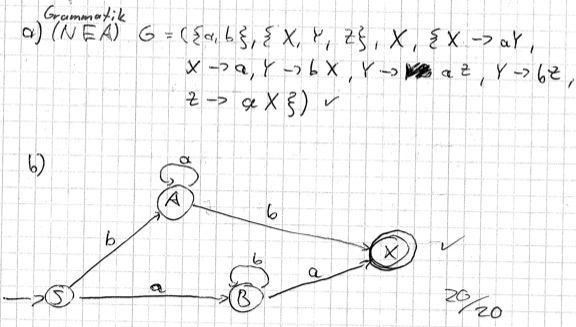
Typ-3-Grammatik versus NEA

1. Gehen Sie entsprechend des Beweises 4.11 vor X und konstruieren Sie eine Grammatik vom Typ 3 für die von dem folgenden NEA akzeptierte Sprache. Geben Sie die Grammatik formal als Quadrupel an. [Graph fehlt in dieser Online-Edition]
2. Gehen Sie entsprechend des Beweises 4.11 vor und konstruieren Sie einen NEA für die durch folgende Grammatik erzeugte Sprache. Zeichnen Sie den NEA.
   G = ({a,b},{S,A,B},S,{S → aB,S → bA,B → a,B → bB,A → b,A → aA})

Kontextfreie Grammatik für Nichtpalindrome
Geben Sie eine kontextfreie Grammatik für folgende Sprache über dem Alphabet {a, b} an.
PAL={w∈{a,b}∗ |w̸=wR}

Chomsky-Normalform
Wandeln Sie die Grammatik G = ({a, b}, {S, A, B, C}, S, R) mit der unten angegebenen Regelmenge R in Chomsky-Normalform um. Führen Sie dazu die drei Schritte der Konstruktion 4.15 durch und geben Sie nach jedem Schritt die entstandene Regelmenge an.
R = {S → ABa,S → CbB,A → CaA,A → a,B → S,B → b,C → Bb,C → A}

Pumping-Lemma für kontextfreie Sprachen
Für ein Wort w ∈ {a,b,c}∗ bezeichnet |w|_a die Anzahl der Buchstaben a im Wort w. Analog definiert man |w|_b und |w|_c.
Beweisen Sie, dass folgende Sprache über dem Alphabet {a, b, c} nicht kontextfrei ist.
L = {w∈{a,b,c}∗ ||w|_a =|w|_b =|w|_c}

nichtreguläre Sprache, die das Pumping-Lemma erfüllt
Zeigen Sie, dass folgende Sprache die Aussage des Pumping Lemmas erfüllt, aber trotzdem nicht regulär ist:
L={w∈{a,b,c}^*|w∈{a,b}^* oder w=cⁱaⁿbⁿ mit i,n≥1}

Fortsetzen berechenbarer Funktionen
Beweisen oder widerlegen Sie: Für jedes f ∈ RAM existiert ein totales g ∈ RAM mit ∀x ∈ Df [f (x) = g(x)].

Differenzen von Kubikzahlen
Liegt die Menge A={d∈N|∃x,y∈N,d=x3 −y3} in RE bzw. REC? Beweisen Sie Ihre Aussagen!